Signal Messenger (X3DH:Extended Triple Diffie-Hellman)

[tk-fuse]

セキュアなメッセンジャーアプリ

Signal Messenger: Speak Freely

開発向けドキュメント

Documentation

X3DH

Specifications >> The X3DH Key Agreement Protocol

If the bundle does not contain a one-time prekey, she calculates:

DH1 = DH(IKA, SPKB)
DH2 = DH(EKA, IKB)
DH3 = DH(EKA, SPKB)
SK = KDF(DH1 || DH2 || DH3)

If the bundle does contain a one-time prekey, the calculation is modified to include an additional DH:

DH4 = DH(EKA, OPKB)
SK = KDF(DH1 || DH2 || DH3 || DH4)

The following diagram shows the DH calculations between keys. Note that DH1 and DH2 provide mutual authentication, while DH3 and DH4 provide forward secrecy.

The Double Ratchet Algorithm

Specifications >> The Double Ratchet Algorithm

Signal-Server

GitHub - signalapp/Signal-Server: Server supporting the Signal Private...

Signal Server Installation Guide

Signal Server Installation Guide

Configuration of Signal Server

Configuration of Signal Server

Maven
https://maven.apache.org/guides/getting-started/index.html#maven-getting-started-guide

---

How Mutual authentication and Forward secrecy in The X3DH Key Agreement Protocol work?

X3DH (Extended Triple Diffie-Hellman) in Go
https://asecuritysite.com/encryption/go_x3dh

With x3dh (Extended Triple Diffie-Hellman), Bob and Alice create key pairs for their long-term identity (IDA and IDB) and publish these to a trusted server (such as WhatsApp or Signal). Next each of them generate a range of pre-shared public keys, and sign them with their private key. In the case of Alice communicating with Bob, then Bob will have a number of pre-shared signed keys. Let’s say the first one is ‘bG, and Alice selects this one. She then calculates three Diffie-Hellman key exchanges with a secret (a’) and her own long term ID (DH1, DH2 and DH3). This is illustrated in the left-hand side of the following graphic:

[tk-fuse]

The X3DH Protocol: A Proof of Security

Ferran_van_der_Have___4104145___The_X3DH_Protocol_-_A_Proof_of_Security.pdf

[tk-fuse]

X3DHプロトコルは、初期セッションの確立時にのみ使用され、共有セッションキーの生成を行います。この共有セッションキーを使用して、双方が安全な通信チャネルを確立します。

注）アプリの再インストールやデバイスの変更をしない限り、同一ユーザ間でのX3DHプロトコルによる共有キー作成のプロセスは行われません。

Signal protocol: when, and why, is X3DH run again between the same two users?

以下のイメージは、1ユーザがアプリで各キーを作成するプロセスを示しています。 ラチェットは、Diffie-Hellman鍵交換（DHの部分）で進行し、その結果を使ってKDFが鍵を生成しますが、KDF自体はラチェット機構とは呼ばれません。KDFはラチェットで得られた鍵素材を基に、次のラチェットやメッセージ暗号化のための具体的な鍵を作成するための派生処理です。図のKDF処理では、送受信のためのキーを作成する際に、同じRoot keyが使用されます。

セッションが確立された後は、通常のDH（Diffie-Hellman）鍵交換を利用して、セッション内のメッセージごとに新しい鍵を生成することで、さらなるセキュリティを確保します。このプロセスが、Signalプロトコルにおける、「Double Ratchetアルゴリズム」です。

Pythonによるcurve25519キー生成（Diffie-Hellman鍵交換）プログラム例

仮想環境下へ移行しライブラリ追加

$ source test/bin/activate
(test) $  pip install cryptography

(test) $ nano curve25519.py

from cryptography.hazmat.primitives.asymmetric import x25519
from cryptography.hazmat.primitives import serialization, hashes
from cryptography.hazmat.primitives.kdf.hkdf import HKDF

# 鍵ペアの生成
def generate_key_pair():
    private_key = x25519.X25519PrivateKey.generate()
    public_key = private_key.public_key()
    return private_key, public_key

# Diffie-Hellman鍵交換の実行
def perform_dh(private_key, peer_public_key):
    shared_key = private_key.exchange(peer_public_key)
    return shared_key

# セッションキーの生成
def derive_session_key(shared_key):
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32,
        salt=None,
        info=b'handshake data',
    )
    session_key = hkdf.derive(shared_key)
    return session_key

# Aliceの鍵ペア生成
alice_private_key, alice_public_key = generate_key_pair()

# Johnの鍵ペア生成
john_private_key, john_public_key = generate_key_pair()

# JohnがAliceの公開鍵を使用してDH鍵交換を行う
john_shared_key = perform_dh(john_private_key, alice_public_key)

# AliceがJohnの公開鍵を使用してDH鍵交換を行う
alice_shared_key = perform_dh(alice_private_key, john_public_key)

# セッションキーの生成
john_session_key = derive_session_key(john_shared_key)
alice_session_key = derive_session_key(alice_shared_key)

# 両者のセッションキーが一致していることを確認
assert john_session_key == alice_session_key

print(f"Alice's Public Key: {alice_public_key.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}")
print(f"John's Public Key: {john_public_key.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}")
print(f"Alice's Shared Session Key: {alice_session_key.hex()}")
print(f"John's Shared Session Key: {john_session_key.hex()}")

実行

(test) $ python3 curve25519.py
  Alice's Public Key: d4d596a41a6df890a609179eb4f79430faed10df3daee39fe71040812d7a7c1e
  John's Public Key: 5ecc6d758f0d993af9c1c7044d640aaccb72b0bfc2764d46db55e2ec1d63d13a
  Alice's Shared Session Key: c02539d5248de4702baacdd5446a4f9b9e68b6526d798858eb8ce2f14f842a58
  John's Shared Session Key: c02539d5248de4702baacdd5446a4f9b9e68b6526d798858eb8ce2f14f842a58

---

Pythonによるcurve25519キー生成（X3DH:Extended Triple Diffie-Hellman鍵交換）プログラム例

(test) $ nano x3dh_curve25519.py

from cryptography.hazmat.primitives.asymmetric import x25519
from cryptography.hazmat.primitives import serialization, hashes
from cryptography.hazmat.primitives.kdf.hkdf import HKDF

# 鍵ペアの生成
def generate_key_pair():
    private_key = x25519.X25519PrivateKey.generate()
    public_key = private_key.public_key()
    return private_key, public_key

# Diffie-Hellman鍵交換の実行
def perform_dh(private_key, peer_public_key):
    shared_key = private_key.exchange(peer_public_key)
    return shared_key

# セッションキーの生成
def derive_session_key(dh_keys):
    concatenated_keys = b''.join(dh_keys)
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32,
        salt=None,
        info=b'x3dh handshake',
    )
    session_key = hkdf.derive(concatenated_keys)
    return session_key

# Aliceの鍵ペア生成
alice_identity_private, alice_identity_public = generate_key_pair()
alice_signed_private, alice_signed_public = generate_key_pair()
alice_one_time_private, alice_one_time_public = generate_key_pair()

# Johnの鍵ペア生成
john_identity_private, john_identity_public = generate_key_pair()
john_ephemeral_private, john_ephemeral_public = generate_key_pair()

# JohnがAliceの公開鍵を使用してDH鍵交換を行う
dh1 = perform_dh(john_ephemeral_private, alice_identity_public)
dh2 = perform_dh(john_ephemeral_private, alice_signed_public)
dh3 = perform_dh(john_ephemeral_private, alice_one_time_public)
dh4 = perform_dh(john_identity_private, alice_signed_public)

# セッションキーの生成
john_session_key = derive_session_key([dh1, dh2, dh3, dh4])

# AliceがJohnの公開鍵を使用してDH鍵交換を行う
dh1_alice = perform_dh(alice_identity_private, john_ephemeral_public)
dh2_alice = perform_dh(alice_signed_private, john_ephemeral_public)
dh3_alice = perform_dh(alice_one_time_private, john_ephemeral_public)
dh4_alice = perform_dh(alice_signed_private, john_identity_public)

# セッションキーの生成
alice_session_key = derive_session_key([dh1_alice, dh2_alice, dh3_alice, dh4_alice])

# 両者のセッションキーが一致していることを確認
assert john_session_key == alice_session_key

print(f"Alice's Public Keys: Identity={alice_identity_public.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}, Signed={alice_signed_public.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}, One-Time={alice_one_time_public.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}")
print(f"John's Public Keys: Identity={john_identity_public.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}, Ephemeral={john_ephemeral_public.public_bytes(encoding=serialization.Encoding.Raw, format=serialization.PublicFormat.Raw).hex()}")
print(f"Shared Session Key: {john_session_key.hex()}")

実行

(test) $ python3 x3dh_curve25519.py
  Alice's Public Keys: Identity=fc9aa611e8172f8c3b72f1d9f1c1f42ff186e26ff5aa2ab045681ab947e98337, Signed=02d3beb7cc5c6ef4c5fb4e5c9e72d84c7281d8d6e4a55dae640719a3c6088e7a, One-Time=3c239d7461a8b5ce4994c4ab27bf0403c17c14a50db10a0beb34147d7e079b67
  John's Public Keys: Identity=4763b080c8c614709d43280b542f2bf459587d7e5cdaeec131d0a18028d15265, Ephemeral=2ccc0f1a49be1e6189c29cac229f5fdcc4a980689894d53d6e2c794b899ed308
  Shared Session Key: eb8ef2a69eb081ff3a8d37687e3e39ad01eeb3c96ec1ac2eeb9a1cbf651ea299

---

仮想環境から退出

(test) $ deactivate

[tk-fuse]

HKDFによる複数の鍵生成

HKDF（HMAC-based Key Derivation Function）は、特に複数の鍵を生成するために適しています。HKDFは、抽出ステップで元の鍵素材から「中間鍵」を生成し、次に拡張ステップでその中間鍵から任意の長さの出力（複数の鍵）を生成します。

たとえば、以下のようにして複数の鍵を導出できます：

• Key1 = HKDF(KM, info1)
• Key2 = HKDF(KM, info2)
• Key3 = HKDF(KM, info3)

ここで、KM は元の鍵素材であり、info1、info2、info3 はそれぞれ異なる用途に対応する識別情報です。この「識別情報（info）」によって、同じ元の鍵素材から異なる鍵を生成することが可能です。

---

セッションキーからルートキー、チェインキー、メッセージキーを生成するPythonコードの例

Signalプロトコルの鍵導出プロセスの概要

1. 初期セッションの確立：

• X3DHプロトコルにより、初期の共有秘密を確立し、その秘密からHKDFを使用して初期セッションキーを導出します。

2. Double Ratchetアルゴリズムの使用：

• ルートキー更新：各ラチェットステップ（例えば、新しいエフェメラルキーの生成）で、HKDFを使用して新しいルートキーを導出します。
• チェインキー更新：各メッセージの送信ごとに、HKDFを使用して新しいチェインキーを生成します。
• メッセージキー生成：チェインキーからHKDFを使用して、各メッセージの暗号化に使用されるメッセージキーを生成します。

session_root_chain_message.py

from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives import hashes
import os

# セッションキー（例としてランダムに生成）
session_key = os.urandom(32)  # 32バイトのランダムなセッションキーを生成する例

# HKDFを使用してルートキーを導出
def derive_root_key(session_key):
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32,  # 生成するキーの長さ
        salt=None,  # オプションのsalt（使用しない場合はNone）
        info=b'root key derivation',  # HKDFに提供する追加情報
    )
    root_key = hkdf.derive(session_key)
    return root_key

# ルートキーからチェインキーを導出
def derive_chain_key(root_key):
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32,
        salt=None,
        info=b'chain key derivation',
    )
    chain_key = hkdf.derive(root_key)
    return chain_key

# チェインキーからメッセージキーを導出
def derive_message_key(chain_key):
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32,
        salt=None,
        info=b'message key derivation',
    )
    message_key = hkdf.derive(chain_key)
    return message_key

# セッションキーからルートキーを導出
root_key = derive_root_key(session_key)

# ルートキーからチェインキーを導出
chain_key = derive_chain_key(root_key)

# チェインキーからメッセージキーを導出
message_key = derive_message_key(chain_key)

print(f"Session Key: {session_key.hex()}")
print(f"Derived Root Key: {root_key.hex()}")
print(f"Derived Chain Key: {chain_key.hex()}")
print(f"Derived Message Key: {message_key.hex()}")

実行

(test) $ python3 session_root_chain_message.py
Session Key: 0ae2f0afb0271ec0e2f9c9f9f1e55c248e5474354cade3b2fd0b711b9bb19622
Derived Root Key: 5e28f1b8dc1e6015113f1434be3f6a55734ecadcfc31517d798f2e8a5187e695
Derived Chain Key: a5685180faf09685068f17b1795ab93d8b9c287eeb0dcebac23080a479b762f3
Derived Message Key: 9fc94e728d17bf23e6eddc245a65c960b937fa2bafd3fc8c778499c952b8e3d8

[tk-fuse]

特徴	対称鍵暗号	非対称鍵暗号
鍵	同一の秘密鍵	公開鍵と秘密鍵
速度	高速	低速
鍵の配布	配布が困難	公開鍵を容易に配布可能
セキュリティ	秘密鍵の管理が重要	秘密鍵が漏洩しない限り安全
用途	大量データの暗号化	鍵交換、デジタル署名、小量データの暗号化

非対称鍵：RK（ルートキー）
対称鍵：CK, A1（チェインキー、メッセージキー）

非対称キーであるRK（Root Key）から作成されるCK（Chain Key）は、非対称キーではなく対称キー。

非対称暗号（公開鍵暗号）は、通常、最初の鍵交換やセッションの初期設定に使用され、その後の通信は対称キー暗号で行われます。これは、対称キー暗号の方が計算効率が高く、より高速な暗号化と復号化が可能だからです。

以下は、そのプロセスの概要：

1. 非対称キーの使用：

• RK（Root Key） は、最初の鍵交換やセッションの設定に使用されます。これは、非対称暗号の一部です。

2. 対称キーの生成：

• 一度安全に通信が確立された後、非対称キーを使用して CK（Chain Key） が生成されます。このChain Keyは対称キーとして使用されます。

3. 対称キーの使用：

• CK（Chain Key）は、対称キー暗号の一部として機能し、メッセージごとに異なるメッセージキーを生成するために使用されます。

---

受信メッセージが飛ばされた場合の処理

PNとNは、ダブルラチェットプロトコルにおいて、メッセージの送信順序と処理状況を追跡するために使われるメッセージ番号です。これらは、メッセージの受信側がメッセージの順番が欠落していたり、順番が入れ替わったりしても適切に処理できるように設計されています。

例：メッセージの欠落や順序の変更

例えば、次のような状況の場合：

1. 送信者が4つのメッセージを送信（B1, B2, B3, B4）。

• メッセージB1を受信者が受け取ったが、B2とB3がスキップされ、B4が先に届いたとします。
• B4が届いた時点で、DHラチェットが進行し、送信チェーンが切り替わります。

2. メッセージB4のヘッダーには次の情報が含まれます：

• PN = 2（前のチェーンで2つのメッセージがスキップされたことを意味します）。
• N = 1（新しい送信チェーンで1つ目のメッセージが送信されたことを示します）。

3. 受信者の処理：

• PN = 2なので、受信者は前のチェーン（B1に対応するチェーン）で、2つのメッセージ（B2とB3）がスキップされたと認識し、それらに対応するメッセージキーを計算し、保存します。
• 同時に、N = 1なので、受信者は新しいチェーンでのメッセージ番号も追跡し、次に受信されるメッセージが順番通りかどうか確認します。

このように、PNとNを使うことで、メッセージが順番通りに届かなかった場合でも、スキップされたメッセージに対応する鍵を保存しておき、後で届いたときに復号できるようにするのがダブルラチェットのメカニズムです。

1. PN (Previous Sending Chain Length)

• PNは、メッセージのヘッダーに含まれており、「送信者が使っていた前回の送信チェーンで生成されたメッセージキーの数」を表します。つまり、前回の送信チェーンが何回メッセージを送信したかという情報を伝えます。
• この情報は、受信者が新しい送信チェーンに切り替わる際（つまり、DHラチェットが進行する際）に、どれだけのメッセージが飛ばされているか（スキップされたか）を把握するために使われます。

2. N (Current Sending Chain Message Number)

• Nは、現在の送信チェーンでのメッセージ番号です。送信者が現在の送信チェーンで送信しているメッセージの順番を示します。各メッセージが送られるごとにNはインクリメント（0, 1, 2, …）されます。
• Nは、受信者がメッセージの順序を把握するのに役立ち、スキップされたメッセージキーを計算して保存するために使われます。

PNとNの働き

• PNは前の送信チェーンの長さを示すので、受信者はそのチェーンで生成されたがまだ受信していないメッセージキーの数を計算できます。
• Nは現在の送信チェーンでのメッセージの位置を示すため、受信者はスキップされたメッセージを追跡し、到着していないメッセージに対する鍵（メッセージキー）を計算して保存しておくことができます。

[tk-fuse]

楕円曲線上の点が何を意味するのか、特にモジュロ演算を含む場合について詳しく説明します（ChatGPT）。

楕円曲線上の点

楕円曲線の方程式は、通常次のような形式を取ります：
y^2 = x^3 + ax + b
ここで、(a) と (b) は定数です。この方程式を満たす (x, y)の組み合わせを楕円曲線上の点と呼びます。

モジュロ演算を含む楕円曲線

モジュロ演算を含む楕円曲線の方程式は、次のように表されます：
y^2 ≡ x^3 + ax + b mod p
ここで、(p) は素数です。これは有限体上の楕円曲線と呼ばれ、特定の有限体 ({F}p 上で定義されています。有限体 {F}p は、0 から (p-1) までの整数を含む集合であり、演算はすべて (p) を法として行われます。

楕円曲線上の点の定義（モジュロ演算を含む場合）

モジュロ演算を含む楕円曲線上の点とは、次の方程式を満たす (x, y) の組み合わせです：
y^2 ≡ x^3 + ax + b \mod p

例：楕円曲線 y^2 ≡ x^3 + x + 1 \mod 11

楕円曲線の方程式：
y^2 ≡ x^3 + x + 1 mod 11

この方程式を満たす (x, y) の組み合わせを求めるためには、次のステップを踏みます：

1. 任意の (x) の値を選ぶ。
2. 右辺の値を計算し、モジュロ11で評価する。
3. その値が平方数（モジュロ11での平方）であるか確認し、対応する (y) の値を見つける。

具体例：(1, 5)

座標 (1, 5) が楕円曲線上の点かどうかを確認するために、方程式に代入します：

1. 右辺の計算：
   1^3 + 1 + 1 = 3
   3 mod 11 = 3

2. 左辺の計算：
   5^2 = 25
   25 mod 11 = 3

右辺と左辺が等しいため：
5^2 ≡ 1^3 + 1 + 1 mod 11
25 ≡ 3 \mod 11
3 ≡ 3 \mod 11

この結果、(1, 5) が楕円曲線 y^2 ≡ x^3 + x + 1 mod 11 上の点であることが確認できます。

楕円曲線上の点の重要性

楕円曲線上の点は、暗号学や数論において重要な役割を果たします。例えば、楕円曲線ディフィー・ヘルマン鍵共有（ECDH）や楕円曲線デジタル署名アルゴリズム（ECDSA）などの暗号アルゴリズムは、楕円曲線上の点を利用して安全な通信やデジタル署名を実現します。

まとめ

楕円曲線上の点とは、特定の方程式を満たす (x, y)の組み合わせであり、モジュロ演算を含む場合でも同様に定義されます。この点が方程式を満たしているということは、その点が曲線の一部であることを意味し、特に暗号学において重要な概念です。

楕円曲線暗号（ECC）において、スカラー倍 (nP) は楕円曲線上の点 (P) に整数 (n) を掛けたものです。ここで、モジュロ演算の関係について詳しく説明します。

楕円曲線と有限体

楕円曲線は通常、有限体 {F}p（ここで (p) は素数）上で定義されます。これは、楕円曲線のすべての計算がモジュロ (p) の演算を含むことを意味します。有限体 {F}p 上の楕円曲線の一般的な形式は次のようになります：

y^2 ≡ x^3 + ax + b mod p

スカラー倍の計算

楕円曲線上の点 (P) に対して、スカラー (n) を掛ける操作 (nP) は、点 (P) を (n) 回足し合わせる操作として定義されます。これには以下のステップが含まれます：

1. 点の加法（Point Addition）
2. 点のスカラー倍（Point Doubling）

これらの操作は、すべてモジュロ (p) の演算として実行されます。

点の加法とスカラー倍

点の加法

楕円曲線上の2点 (P = (x_1, y_1)) と (Q = (x_2, y_2)) の加法 (R = P + Q = (x_3, y_3)) は次のように計算されます：

1. P ≠ Q の場合：

   λ = (y2 - y1)/(x2 - x1) mod p

   x3 = λ^2 - x1 - x2 mod p

   y3 = λ(x1 - x3) - y1 \mod p

2. P = Q の場合（スカラー倍）：

   λ = (3x1^2 + a)/(2y1） mod p

   x3 = λ^2 - 2x1 mod p

   y3 = λ(x1 - x3) - y1 mod p

秘密鍵と公開鍵

ECCの文脈で、次のように秘密鍵と公開鍵が定義されます：

• 秘密鍵 (n)：これはランダムに選ばれた整数で、秘密に保持されます。
• 公開鍵 (Q)：これは、基準点 (G) に対するスカラー倍 (nG) によって計算されます。

公開鍵の計算は次のようになります：
Q = nG

この操作もすべてモジュロ (p) の演算として実行されます。

モジュロの関係

スカラー倍の計算 (nP) には、モジュロ (p) の演算が関係します。具体的には、各ステップでの計算がモジュロ (p) で行われます：

1. 点の加法やスカラー倍のための中間計算での分数や乗算はすべてモジュロ (p) で計算されます。
2. 最終的な結果の座標 (x, y) もモジュロ (p) での値になります。

まとめ

楕円曲線上の点 (P) に対するスカラー倍 (nP) は、モジュロ (p) の演算を含む一連の点の加法とスカラー倍の結果として計算されます。このプロセスを通じて、秘密鍵 (n) と公開鍵 (Q = nG) の間に強いセキュリティを提供する数学的な関係が確立されます。これにより、暗号システムの堅牢性が保証されます。

[tk-fuse]

参考サイト

ECDH ( Elliptic Curve Diffie-Hellman)

Elliptic Curve Diffie-Hellman (ECDH)

以下のサイトは、楕円曲線とモジュロ演算について視覚的に分かりやすく説明しています。楕円曲線上の任意の座標は、モジュロ演算により、0と正の整数から成る座標に変換されます。

The Animated Elliptic Curve

Hands-on: X25519 Key Exchange

グラフ計算機

Desmos | グラフ計算機

Elliptic Curves for Security

https://www.ietf.org/rfc/rfc7748.txt

Table of Contents

1. Introduction . . . . . . . . . . . . . . . . . . . . . . . . 2
2. Requirements Language . . . . . . . . . . . . . . . . . . . . 3
3. Notation . . . . . . . . . . . . . . . . . . . . . . . . . . 3
4. Recommended Curves . . . . . . . . . . . . . . . . . . . . . 4
   4.1. Curve25519 . . . . . . . . . . . . . . . . . . . . . . . 4
   4.2. Curve448 . . . . . . . . . . . . . . . . . . . . . . . . 5
5. The X25519 and X448 Functions . . . . . . . . . . . . . . . . 7
   5.1. Side-Channel Considerations . . . . . . . . . . . . . . . 10
   5.2. Test Vectors . . . . . . . . . . . . . . . . . . . . . . 11
6. Diffie-Hellman . . . . . . . . . . . . . . . . . . . . . . . 14
   6.1. Curve25519 . . . . . . . . . . . . . . . . . . . . . . . 14
   6.2. Curve448 . . . . . . . . . . . . . . . . . . . . . . . . 15
7. Security Considerations . . . . . . . . . . . . . . . . . . . 15
8. References . . . . . . . . . . . . . . . . . . . . . . . . . 16
   8.1. Normative References . . . . . . . . . . . . . . . . . . 16
   8.2. Informative References . . . . . . . . . . . . . . . . . 17
   Appendix A. Deterministic Generation . . . . . . . . . . . . . . 19
   A.1. p = 1 mod 4 . . . . . . . . . . . . . . . . . . . . . . . 20
   A.2. p = 3 mod 4 . . . . . . . . . . . . . . . . . . . . . . . 21
   A.3. Base Points . . . . . . . . . . . . . . . . . . . . . . . 21
   Acknowledgements . . . . . . . . . . . . . . . . . . . . . . . . 22
   Authors’ Addresses . . . . . . . . . . . . . . . . . . . . . . . 22

[tk-fuse]

Comparison of cryptography libraries

Elliptic-curve cryptography (ECC) support

Further information: Elliptic-curve cryptography

Implementation	NIST	SECG	ECC Brainpool	Curve25519	Curve448	GOST R 34.10[36]	SM2
Botan	Yes	Yes	Yes	Yes	No	Yes	Yes
Bouncy Castle	Yes	Yes	Yes	Yes	No	Yes	No
BSAFE	Yes	Yes	No	No	No	No	No
cryptlib	Yes	Yes	Yes	No	No	No	No
Crypto++	Yes	Yes	Yes	Yes	No	No	No
GnuTLS	Yes	No	No	No	No	No	No
Java’s default JCA/JCE providers	Yes	Yes	No	Yes	Yes	No	No
Libgcrypt	Yes	Yes	Yes	Yes	Yes	Yes	Yes
libsodium	Yes	No	No	Yes	Yes	No	No
Mbed TLS	Yes	Yes	Yes	Yes	No	No	No
Nettle	Yes	Partial	No	Yes	No	No	No
OpenSSL	Yes	Yes	Yes	Yes	Yes	Yes	Yes
wolfCrypt	Yes	Yes	Yes	Yes	Yes	No	No

[tk-fuse]

AES-GCMとHMAC-SHA256とHKDFを相互に関連付けて説明 —> ChatGPTによる回答

AES-GCM、HMAC-SHA256、HKDFは、それぞれ異なる目的を果たしつつ、セキュアな通信プロトコル（例えば、Signalなど）で連携して機能しています。それぞれの役割を相互に関連付けながら、暗号通信全体でどのように使われているか説明します。

1. HKDF（鍵導出関数）: 鍵を生成する役割

HKDF（HMAC-based Key Derivation Function）は、セキュアな共有鍵をさまざまな用途に使えるように派生させる鍵導出関数です。通常、ECDH（Diffie-Hellman）などの鍵交換プロトコルによって1つの共有鍵（Input Key Material: IKM）が生成されますが、この単一の鍵を直接使うのは安全性に問題がある場合があります。そこで、HKDFを使って、以下のような異なる目的に応じた鍵を派生させます。

• 暗号化に使うAES鍵（AES-GCMでのメッセージ暗号化に使用）
• メッセージ認証に使うHMAC鍵（HMAC-SHA256でメッセージの完全性確認に使用）

この鍵導出は、2段階で行われます。

• 抽出フェーズ: 共有鍵（IKM）から擬似ランダムな鍵（PRK）を生成。
• 拡張フェーズ: PRKを元に、必要な長さと数の鍵を生成。

こうして生成された鍵が、暗号化や認証に使われます。

2. AES-GCM（認証付き暗号化方式）: メッセージを暗号化し、認証する役割

AES-GCM（Galois/Counter Mode）は、認証付き暗号化を行うモードで、AES（Advanced Encryption Standard）をベースとしています。このアルゴリズムは、メッセージを暗号化しながら、**改ざん検出（認証）**も同時に行います。具体的には次のように機能します。

• AES暗号化: HKDFで生成された鍵の1つがAES-GCMの暗号鍵として使われ、メッセージの暗号化が行われます。
• 認証タグの生成: AES-GCMは、メッセージの一部として認証タグを生成します。このタグは、受信者がメッセージの改ざん検出に使用します。

AES-GCM自体には暗号化と簡単な認証機能が組み込まれているため、通常はHMACによる追加の認証が不要です。ただし、AES-GCMとHMAC-SHA256の役割は異なる場面で使い分けられることがあります。

3. HMAC-SHA256（メッセージ認証コード）: メッセージの完全性を保証する役割

HMAC-SHA256は、メッセージの認証と改ざん検出に使われる技術です。AES-GCMとは異なり、HMAC-SHA256はメッセージそのものを暗号化する機能はありませんが、メッセージが改ざんされていないかどうかを保証します。

• 認証鍵: HKDFで生成された別の鍵が、HMAC-SHA256で使用されます。この鍵とメッセージを使ってHMACを生成し、メッセージに付加します。
• 受信者が認証: 受信者は同じ鍵でHMACを再計算し、メッセージに付加されたHMACと一致するかを確認します。これにより、メッセージが改ざんされていないことを確認できます。

4. 相互の関連付け: これらの技術がどのように連携しているか

ここでは、これらの技術がどのように一連の暗号通信プロトコル内で使われるか、例を挙げて説明します。

例: Signalのメッセージ暗号化プロセス

1. 鍵交換とHKDFによる鍵導出:

   • Signalでは、X3DHプロトコルやDouble Ratchetアルゴリズムによって共有鍵（IKM）が確立されます。
   • このIKMから、HKDFを使って複数の鍵を派生させます。これには、メッセージの暗号化に使うAES鍵や、メッセージ認証に使うHMAC鍵が含まれます。

2. AES-GCMでメッセージを暗号化:

   • HKDFで生成されたAES鍵を使用し、メッセージをAES-GCMモードで暗号化します。これにより、メッセージの機密性が保たれます。
   • AES-GCMは、メッセージの認証タグも生成します。これにより、暗号化されたメッセージに対して、改ざん検出も行われます。

3. HMAC-SHA256でメッセージの認証（場合によっては）:

   • さらに、HMAC-SHA256を使ってメッセージ認証を行うこともあります。AES-GCMの認証タグとは別に、HMAC-SHA256を使ってメッセージの完全性を検証する場合があります。
   • HKDFで生成されたHMAC鍵を使い、メッセージからHMACを生成し、受信者がそのHMACを検証します。

4. 受信者がメッセージを復号:

   • 受信者は、HKDFで同じ鍵を導出し、AES-GCMを使ってメッセージを復号します。
   • AES-GCMの認証タグを検証し、さらにHMAC-SHA256も確認することで、メッセージが改ざんされていないことを確認します。

まとめ

• HKDFは、共有鍵から暗号化鍵や認証鍵を導出し、それぞれの用途に応じた鍵を生成します。
• AES-GCMは、HKDFで生成された暗号化鍵を使ってメッセージを暗号化し、認証タグを生成することで、暗号化と同時にメッセージの改ざん検出も行います。
• HMAC-SHA256は、別のHKDFで生成された鍵を使って、メッセージの完全性をさらに強固に保証するために使用されます。

これらの技術は、相互に連携し、機密性、完全性、認証を確保した安全なメッセージ交換を実現します。

[tk-fuse]

Signalのメッセージ暗号化プロトコルでは、AES-GCMとHMAC-SHA256の両方が使用されていますが、それぞれ異なる役割を担っており、互いに補完的に働いています。Signalは、Double Ratchetアルゴリズムに基づいて、メッセージの暗号化と認証を行います。具体的には、次のような方法でAES-GCMとHMAC-SHA256が関連付けられています。

SignalでのAES-GCMの役割

Signalのメッセージ暗号化では、AES-GCMがメッセージの暗号化とメッセージ認証の両方に使用されます。AES-GCMは、メッセージの機密性（暗号化）を保つだけでなく、認証タグを生成することでメッセージの完全性（改ざん検出）も保証します。

1. AES-GCMで暗号化:
   • 各メッセージは、ランダムに生成されたAES鍵を使ってAES-GCMモードで暗号化されます。
   • AES-GCMは暗号化されたメッセージとともに認証タグを生成し、これをメッセージに付加します。このタグによって、メッセージが改ざんされていないかを確認します。

SignalでのHMAC-SHA256の役割

AES-GCMの認証機能があるにもかかわらず、Signalプロトコルはメッセージ認証のために追加でHMAC-SHA256を使用します。これは、メッセージの完全性をさらに強固に保証し、よりセキュアな通信を提供するためです。

2. HMAC-SHA256でメッセージ認証:

   • Signalは、メッセージそのものの認証のために、AES-GCMで暗号化されたデータに対してさらにHMAC-SHA256を適用します。
   • これにより、AES-GCMによる認証タグに加え、HMAC-SHA256でもメッセージの認証を行い、通信のセキュリティを二重に確保しています。

3. Double RatchetとHMAC:

   • SignalのDouble Ratchetアルゴリズムは、各メッセージごとに新しい鍵を導出する仕組みです。この中で、HKDFを使って、AES-GCMに使用する暗号化鍵や、HMAC-SHA256に使用する認証鍵が生成されます。
   • このプロセスにより、メッセージごとに異なる鍵が使用され、セキュリティが大幅に向上します。

なぜSignalはHMAC-SHA256を追加で使うのか？

SignalがAES-GCMだけでなく、HMAC-SHA256も使ってメッセージ認証を行う理由は、以下の通りです：

• 二重の認証: HMAC-SHA256はAES-GCMの認証タグと異なる暗号手法でメッセージの完全性を確認するため、万が一AES-GCMの認証機能に脆弱性が発見されたとしても、HMAC-SHA256が別の方法で完全性を保証します。
• より強力なセキュリティ: HMAC-SHA256は、より高い信頼性を持つメッセージ認証コードを生成するため、認証の強化が図られます。
• プロトコルの一貫性: Signalプロトコルは非常に複雑で、多段階の鍵導出と暗号化・認証の仕組みを用いています。これにより、通信が常に最新のセキュリティ標準に基づいて確実に保護されます。

SignalにおけるAES-GCMとHMAC-SHA256の流れ

1. メッセージの暗号化:

   • メッセージは、Double Ratchetアルゴリズムで生成された鍵を使ってAES-GCMで暗号化され、暗号文と認証タグが生成されます。

2. メッセージの認証:

   • 生成された暗号文に対して、さらにHMAC-SHA256で認証コード（HMACタグ）が計算され、暗号文と共に送信されます。

3. 受信者による復号と検証:

   • 受信者は、AES-GCMの認証タグを使ってメッセージが改ざんされていないか確認し、さらにHMAC-SHA256の認証タグを使って追加の確認を行います。

まとめ

• AES-GCMは、Signalメッセージの暗号化と認証タグの生成に使用されます。
• HMAC-SHA256は、暗号化されたメッセージ全体に対してさらに追加の認証タグを生成し、メッセージの完全性を二重に保証します。
• Signalでは、AES-GCMの認証機能に加えてHMAC-SHA256を使うことで、セキュリティを強化しています。これにより、メッセージの機密性・完全性・認証のすべてを高度に確保しています。

このように、SignalプロトコルはAES-GCMとHMAC-SHA256を相互に活用して、非常に強力なセキュリティを提供しています。

[tk-fuse]

以下ブログ記事からの転載

Flexisip X3DH (Extended Triple Diffie-Hellman) Public Key Server - FICUSONLINE F9E

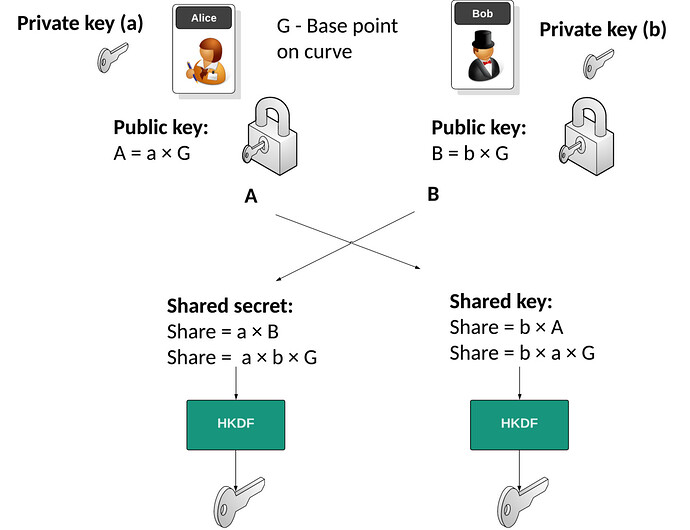
X3DH (Extended Triple Diffie-Hellman) とECDH(Elliptic Curve Diffie-Hellman)について

メッセージ暗号化

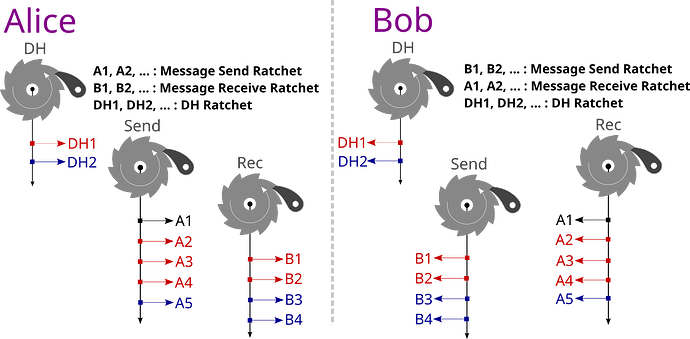
Linphoneが採用しているメッセージの暗号化(LIME)には、Signalが公開している以下のプロトコルが採用されています。X3DHは共有鍵を生成する手順であり、ダブルラチェットは、X3DHプロトコルで生成された共有鍵を用いて、メッセージの暗号化および復号に使用する新しい鍵を生成・更新する手順です。

1. X3DH(Extended Triple Diffie-Hellman)
2. ダブルラチェット(Double-Ratchet)

暗号化に使用される鍵そのものは、幾何学的な楕円曲線上のX座標（モジュロ演算後の座標）であり、X3DHやダブルラチェットでは、演算効率とセキュリティのバランスを考慮した以下の楕円曲線が利用されています。

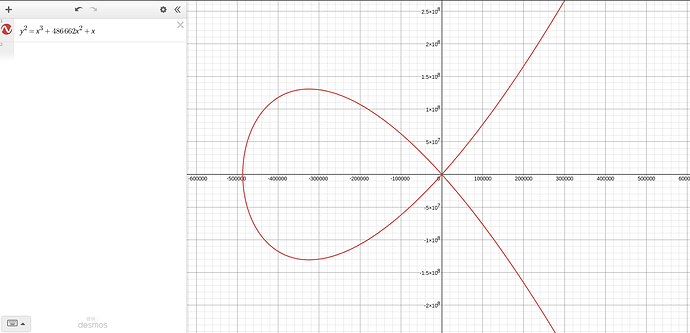
Curve25519 (𝐸 ∶ 𝑦² = 𝑥³ + 486662𝑥² + 𝑥 and 𝑝 = 2²⁵⁵ − 19)

または、

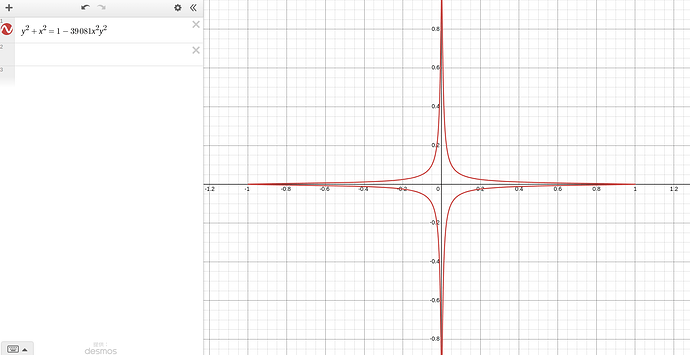
Curve448 (𝐸 ∶ 𝑦² + 𝑥² = 1 − 39081𝑥²𝑦² and 𝑝 = 2⁴⁴⁸ − 2²²⁴ − 1)

X3DH（Extended Triple Diffie-Hellman）

ECDH(Elliptic Curve Diffie-Hellman)は楕円曲線上の座標を利用した共有鍵生成アルゴリズムで、X3DHはそれを拡張したもの。共有鍵を生成するための鍵が幾つか追加され、プロセスが多段になっています。

X3DHは、主に初めて通信を行う二者間で、安全に暗号鍵を交換し、後続のメッセージ暗号化に必要な「セッション鍵」を確立するために使用されます。具体的には、初回の鍵交換および信頼関係の確立に関わるプロセスでX3DHが使われます。

X3DHは次のプロセスにおいて重要な役割を果たします。

1. 初回の鍵交換（初めて通信を開始する際）

利用者同士が初めてメッセージを送る際、どちらの利用者も相手の公開鍵をまだ知らない状態です。このとき、X3DHを使って安全な鍵交換を行い、暗号化されたメッセージを交換できるようにします。この初回の鍵交換によって、両者の間にセッション鍵が生成され、その後のメッセージが暗号化されます。

X3DHは、次の4つの鍵を使って安全な鍵交換を実現します。

長期公開鍵（Identity Key, IK）:

各ユーザーが事前に生成しておき、他のユーザーに公開する公開鍵。これによって通信相手のアイデンティティを識別できます。

署名付き一時公開鍵（Signed PreKey, SPK）:

各ユーザーが公開する一時的な公開鍵で、長期公開鍵で署名されています。これは、中間者攻撃を防ぐために重要です。

一時的公開鍵（One-Time PreKey, OPK）:

一度しか使わない一時的な公開鍵。この鍵は、通信の秘匿性を強化するために用意されており、すでに交換されているかもしれない他の鍵とは独立したものです。

送信者のエフェメラル鍵（Ephemeral Key, EK）:

メッセージ送信時に一時的に生成される鍵で、セッションの際に使用されます。

2. X3DHによる鍵交換プロトコルの流れ

X3DHは、次の手順で安全な鍵交換を行います。

公開鍵の受け取り:

メッセージ送信者（Alice）は、受信者（Bob）の公開鍵セット（Identity Key、Signed PreKey、One-Time PreKey）をX3DHサーバーから取得します。

• Aliceは、Bobの長期的な公開鍵Identity Keyを使ってSigned PreKeyの署名を検証 —> DH1

Diffie-Hellman鍵交換:

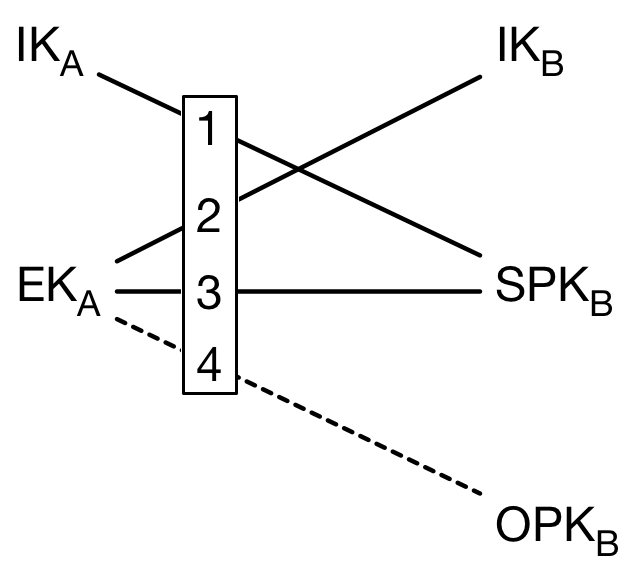
Aliceは、自身のエフェメラル鍵（EK）を生成し、Bobの公開鍵と共に、次の3つのDiffie-Hellman鍵交換を実行します（下図参照）。

• Aliceのエフェメラル鍵とBobのIdentity Key —> DH2
• Aliceのエフェメラル鍵とBobのSigned PreKey —> DH3
• Aliceのエフェメラル鍵とBobのOne-Time PreKey —> DH4

これにより、共有の秘密情報が生成されます。この秘密情報をもとにして、暗号鍵が導出されます。

鍵の導出（Key Derivation）:

Diffie-Hellman鍵交換で得られた秘密情報を入力として、HKDF（HMAC-based Key Derivation Function）を使用して、共有のセッション鍵が導出されます。この鍵を使って、その後の通信を暗号化します。
セッション鍵の確立:

こうして確立されたセッション鍵は、その後のメッセージ送信に使用されます。初回のメッセージがこの鍵で暗号化され、受信者は自分の秘密鍵を使って復号します。

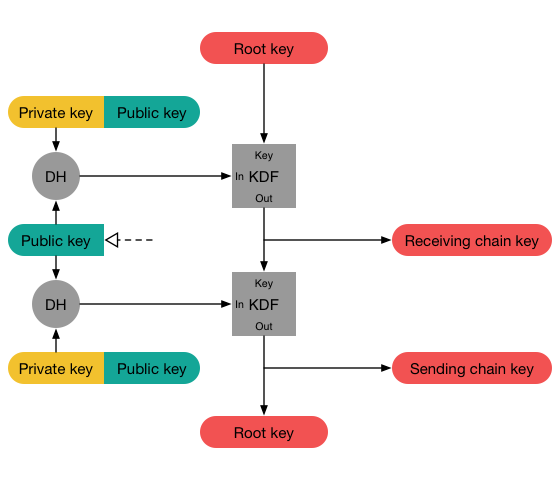
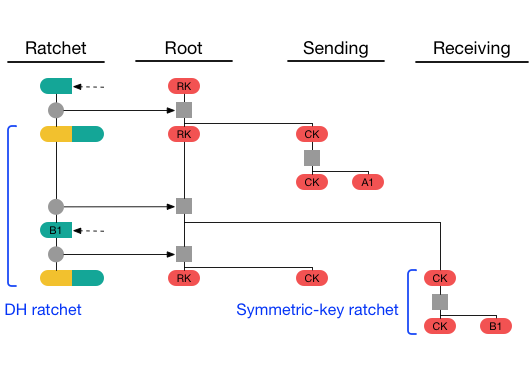
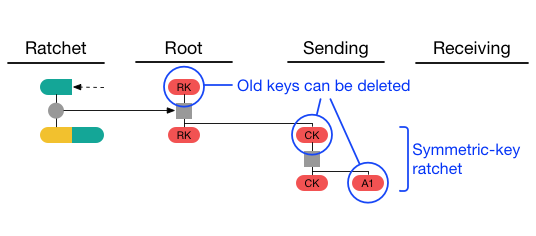
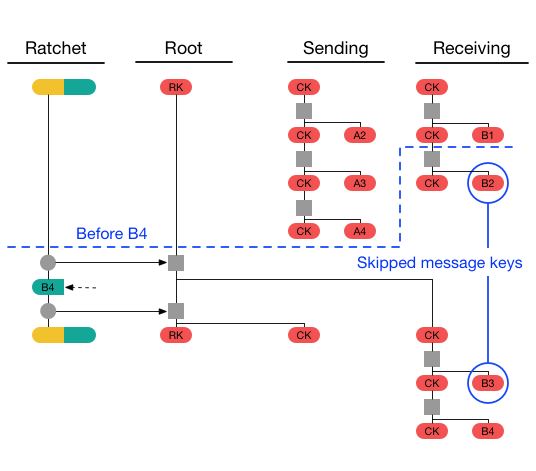
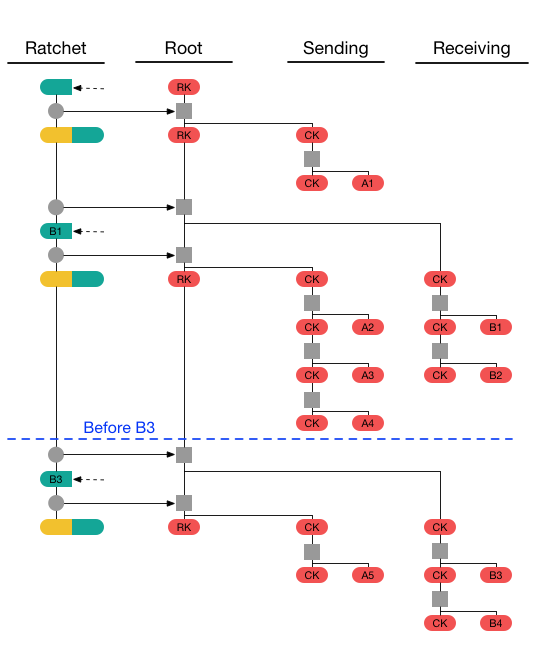
3. 後続の通信とDouble Ratchetプロトコルとの連携

X3DHで初回の鍵交換が完了すると、その後の通信はダブルラチェットプロトコルによって管理されます。ダブルラチェットプロトコルは、メッセージごとに新しい鍵を生成し、より高いセキュリティを提供します。X3DHで確立されたセッション鍵が、ダブルラチェットの初期鍵として使用され、以後のメッセージごとの鍵はダブルラチェットの仕組みによって更新されます。

---

X3DHにおけるEdDSAの役割

EdDSAを使う場合、署名の対象は必ず何かしらのデータである必要があります。署名の対象はメッセージ本文に限定されず、鍵自体や鍵の属性なども署名対象として扱います。

EdDSA（LinphoneのLIMEではXEdDSAではなくEdDSAが使用されています）は、次の場面で使用されます。

Edwards-Curve Digital Signature Algorithm (EdDSA)

1. Signed PreKeyの署名

Signed PreKeyは、各ユーザーがサーバーにアップロードしておく一時的な公開鍵で、X3DHプロトコルの鍵交換で利用されます。
このPreKeyが第三者によって改ざんされないように、ユーザーの長期Identity Key（IDキー）でEd25519署名を施します。この署名により、他者がSigned PreKeyを勝手に差し替えたり、改ざんすることを防ぎます。

2. 署名の検証 DH1

鍵交換を開始する際、メッセージの送信者（Alice）は受信者（Bob）のSigned PreKeyをサーバーから取得します。
Aliceは、Bobの長期Identity Keyで、このSigned PreKeyに施されたEd25519署名を検証します。この検証プロセスにより、Signed PreKeyが確かにBobによって生成されたものであり、改ざんされていないことが確認されます。

---

メッセージを送受信するAliceとBobの双方で以下定義する鍵により共有鍵を生成します。

• Alice’s identity key IKA

• Alice’s ephemeral key EKA

• Bob’s identity key IKB

• Bob’s signed prekey SPKB

• Bob’s prekey signature Sig(IKB, Encode(SPKB))

• (Optionally) Bob’s one-time prekey OPKB

DH1 = DH(IKA, SPKB)
DH2 = DH(EKA, IKB)
DH3 = DH(EKA, SPKB)
SK = KDF(DH1 || DH2 || DH3)

または、

DH1 = DH(IKA, SPKB)
DH2 = DH(EKA, IKB)
DH3 = DH(EKA, SPKB)
DH4 = DH(EKA, OPKB)
SK = KDF(DH1 || DH2 || DH3 || DH4)

ECDH(Elliptic Curve Diffie-Hellman)

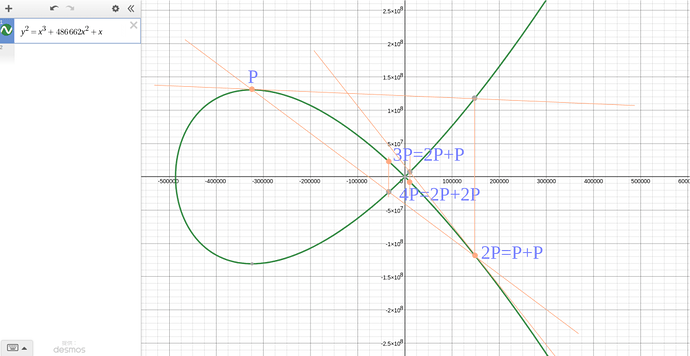
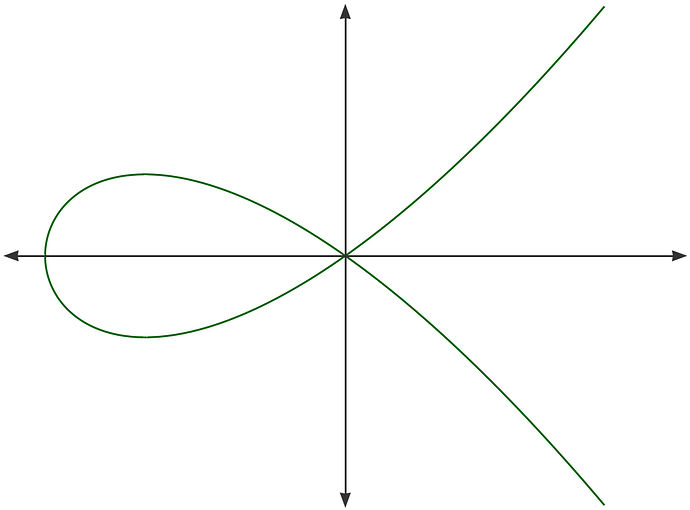
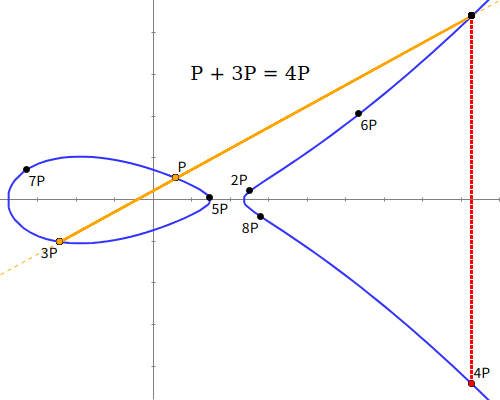
ECDHで利用される楕円曲線上の任意の2点P,Qを結ぶ直線（または任意の点Pにおける接線）が、楕円曲線自身と交わる点R’をX軸に対して反転させた点をRとした場合、P+Q=R（接線の場合はP+P=2P=R）が幾何学的に楕円曲線上で成立するとします。この点の演算をそれぞれ、

• P+Q=R：点の加法（Point Addition)、
• P+P=2P=R：点のスカラー乗算（Point Doubling）

と定義します。

上記のルールに従うと、R=2Pにおける接線が再び楕円曲線と交わる点のX軸に対して反転させた点が2P+2P=4Pと定義できます。同じようにして点4Pにおける接線から4P+4P=8Pの点を定義できます。

ここまでで点P,2P,4P,8Pが定義できました。この各点から、例えば点3Pは、点Pと点2Pを結んだ直線が再び楕円曲線と交わる点のX軸に対して反転させた点と定義できます。このように点のスカラー乗算と加法を効率的に利用することで、2P+4P=6P、4P+8P=12P、この12Pから12P+8P=20Pなど各点の演算を効率的に行うことができます。

楕円曲線と各点の演算について、下記サイトが分かりやすく纏めています。

The Animated Elliptic Curve

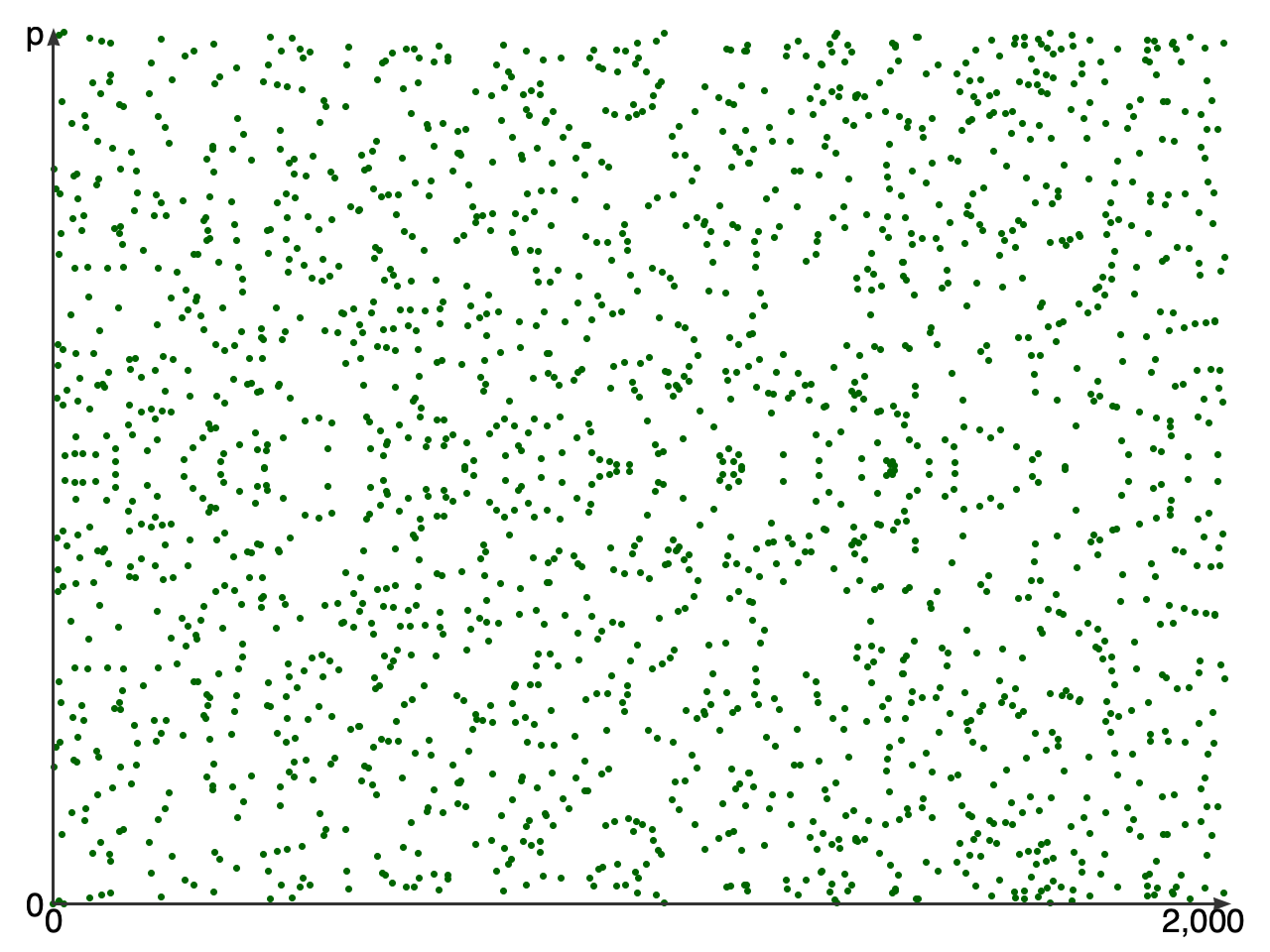
ECDHでは、実際の楕円曲線上の任意の点を直接利用する訳ではありません。各点の座標が割り切れない小数や無限遠点を扱うことになってしまい非現実的です。そのため、楕円曲線の方程式の両辺をモジュロ演算し、その演算結果が等しくなる点(x,y)の集合体に変換します。以下のイメージです。

上記の楕円曲線Curve25519上の任意の点を、モジュロ演算により有限領域にプロット（一部抜粋）。

点の総数は、

n = 2²⁵² + 27742317777372353535851937790883648493

となります。

Curve25519のECDHでは、点が不規則にプロットされるため（ただしy=p/2の直線に対し線対称）、起点Pおよび双方（倍率aとbを秘密鍵として使用）の共有点 aP や bP が第三者に知られても、(a+b)P を計算することは容易ですが、 abP を特定することは実質的に不可能です。これは、楕円曲線離散対数問題が非常に困難であり、n が天文学的に大きい数であるためです。

Curve25519のECDHで生成される具体的な共有鍵の例として、起点Pを

P=( 9 , 14781619447589544791020593568409986887264606134616475288964881837755586237401 )

とした場合、AliceとBob各々が秘密鍵を定義し公開鍵を相互に交換することで共有鍵を生成します。このCurve25519を採用した鍵交換プロトコルがX25519です。

---

秘密鍵（P点のスカラー倍率）

Bob private (b):	19606234678399378633456480350841655717034562515722490628739051202331311643228
Alice private (a): 	109204347234327284008793236257980475297107461097776439083128173099763401227175

---

公開鍵（スカラー倍率で乗算した点aPと点bPのX座標）

Bob public (bP):	 b'34c2b65e53c2877a7321c29ac3a1c2bac29d3721c29fc3bb44c291c392c28dc38574c38d7562c3bf71c39fc2a4c3aec2b973'
Alice public (aP):	 b'c2a307c384c3b9c39f64067cc3b724c290c3a818c28fc2abc2aa151d0a3e2c2c42c38cc28f4e3f0e1d54c2a744'

---

共有鍵（AliceとBobがそれぞれの秘密鍵と公開鍵をスカラー乗算した点のX座標）

Bob shared (b)aP:	 b'c382c2ba19c3b1c39142c38ec39161c2b93251c390c2876ac2b477c3bf6ec28740c2a7c387c283c2be6ec2b1c28bc3a32dc3a128'
Alice shared (a)bP:	 b'c382c2ba19c3b1c39142c38ec39161c2b93251c390c2876ac2b477c3bf6ec28740c2a7c387c283c2be6ec2b1c28bc3a32dc3a128'

X25519の使用される各鍵サイズは32バイト（256ビット）ですが、様々なセキュリティ上の懸念事項に対処するため、以下の5ビットの値は固定されています。

Bits	Value	Reason
0,1,2	0	Protect against small-subgroup attacks, which would allow one peer to use a manipulated secret key to discover the other peer’s secret key
254	1	Prevent implementors from skipping a multiplication round for smaller keys, which would expose a timing leak
255	0	Constrain n < 2²⁵⁵, which prevents the algorithm from reaching the “infinity” result for base-point x=9

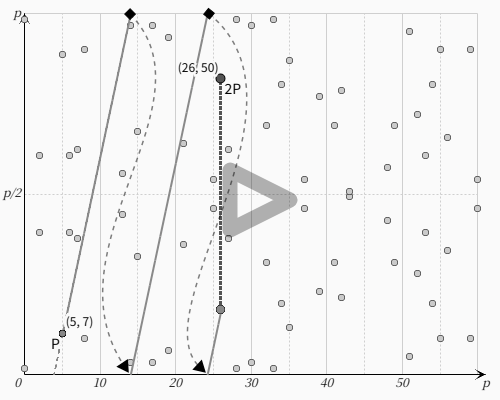
以下は、楕円曲線をモジュロ演算した有限領域における点の演算方法の具体例です。起点P(X0,Y0)を(5,7)とします。この点の接線から2Pを算出します。

y²=x³+9x+1 mod 61

点Pにおける接線の傾きλは、両辺を微分して

2y･dy/dx=3x²+9
λ=dy/dx=(3x²+9)/2y=(325+9)/27=42/7=6 mod 61 = 6

2P(X1,Y1)の座標は、

X1=λ²-2X0=36-25=26 mod 61 = 26
Y1=λ(X0-X1)-Y0=6(5-26)-7=6(-21)-7=-126-7=-133 mod 61 = (-61*2-11) mod 61 = -11 mod 61 = 50

よって2P(26,50)となります。

同様にして点2Pの接線とその座標から点4P、点4Pの接線とその座標から点8P、以下、点16P、点32P、点64P、点128P…が算出できます。

倍加と加算アルゴリズム (Double and Add Algorithm)

スカラー倍kをバイナリ変換（2進数）すると点kPの演算を効率的に行えます。ビット単位でスカラー値を扱い、各ビットに対して「倍加（Double）」と「加算（Add）」の操作を繰り返します（実用上、モンゴメリーラダーというサイドチャネル攻撃（タイミング攻撃や電磁放射攻撃など）に強いアルゴリズムが使用されます）。

ビットが1の場合は「倍加+加算」、ビットが0の場合は「倍加のみ」を行います。

例えば k=151の場合、そのバイナリは、10010111 となります。よって、

151P =
(2⁷x1+2⁶x0+2⁵x0+2⁴x1+2³x0+2²x1+2¹x1+2⁰x1)P

• ビット0：点Pそのものを表します。
• ビット1：1 点の倍加2Pと点の加算2P+P
• ビット2：1 点の倍加4Pと点の加算4P+2P+P
• ビット3：0 点の倍加8P
• ビット4：1 点の倍加16Pと点の加算16P+4P+2P+P
• ビット5：0 点の倍加32P
• ビット6：0 点の倍加64P
• ビット7：1 点の倍加128Pと点の加算128P+16P+4P+2P+P=151P

7回の倍加と4回の加算で処理できます。

[tk-fuse]

以下ブログ記事の転載です。

Double Ratchet Algorithm - FICUSONLINE F9E

ダブルラチェットプロトコルにおける鍵交換と鍵生成の仕組み

X3DHで初回の鍵交換が完了すると、その後の通信はダブルラチェットプロトコルによって管理されます。ダブルラチェットプロトコルは、メッセージごとに新しい鍵を生成し、より高いセキュリティを提供します。

X3DHで確立されたセッション鍵は、ダブルラチェットプロトコルのルートキーとなり、以降のすべての鍵交換とメッセージ暗号化プロセスの基礎となります。ルートキーから派生するチェーンキーが、各メッセージに使われる暗号鍵を生成し、セキュアな通信が維持されます。

DHラチェットアルゴリズム（The Double Ratchet Algorithm）

1. DH鍵交換（Diffie-Hellman）

図の左側にある2つの鍵ペア（Private key と Public key）が、Diffie-Hellman（DH）鍵交換に使われます。通信の参加者が、互いの公開鍵と自分の秘密鍵を使用して共有鍵を生成します。この共有鍵は第三者に知られることなく安全に共有されます。

Private key : メンバーの秘密鍵。各ラチェットステップで更新され、新しい鍵ペアを生成。

Public key : 相手に公開される鍵。これを使って双方が共有鍵を生成。
DH: 相手の公開鍵と自分の秘密鍵を使って共有鍵を生成。この共有鍵は、KDFの入力に使われます。

2. KDF（鍵導出関数）

図の中央にあるKDFは、共有鍵や他の鍵（ルートキーなど）から新しい鍵を生成するための関数です。

Key, In : 共有鍵（DH鍵交換の結果）と既存のルートキーが入力されます。

Out : KDFからは、次に使う新しい鍵が導出されます。ここでは、新しいルートキーと、送信チェーンキーまたは受信チェーンキーが生成されます。

KDFを使うことで、鍵が毎回更新され、攻撃者が過去の鍵を手に入れても未来のメッセージが保護され続ける「前方秘匿性」が保証されます。

3. ルートキー（Root Key）

図の最上部と最下部にあるルートキーは、KDFによって更新され、次のラチェットステップで再び使われます。ルートキーは、暗号通信の最初から続いている基本的な鍵であり、KDFの計算によって常に新しく更新されます。

4. 送信チェーンキーと受信チェーンキー

図の右側に示されている送信チェーンキーと受信チェーンキーは、それぞれメッセージの暗号化に使われる鍵です。

送信チェーンキーは、メッセージを送る際に使用される鍵です。
受信チェーンキーは、メッセージを受け取る際に使用される鍵です。

送信側と受信側で異なるチェーンキーが生成されることで、送信と受信のセキュリティが独立して保たれます。

---

ダブルラチェットプロトコル（Double Ratchet Protocol）

ダブルラチェットの「ダブル」とは、2つの異なるラチェット機構を指しています。このプロトコルは、通信の安全性を高めるために2種類の鍵生成メカニズム（ラチェット）を組み合わせています。

1. 対称鍵ラチェット（Symmetric-key Ratchet）

対称鍵（送受信）ラチェットは、既存の対称鍵（セッション鍵）をもとに、新しい鍵を生成するメカニズムです。新しいメッセージを送るたびに、以前の鍵から次の鍵が生成されます。これにより、過去の鍵が漏洩しても新しい鍵は守られる「前方秘匿性（forward secrecy）」が確保されます。

• メッセージごとに鍵を更新
• メッセージが送受信されるたびに鍵を更新することで、各メッセージを個別に保護

2. 公開鍵ラチェット（Public-key Ratchet）

公開鍵（DH）ラチェットは、セッション中に新しい鍵交換を行うために使用されます。この鍵交換は非同期で行われ、片方のユーザーが新しい鍵ペアを生成して相手に公開鍵を送信します。これにより、長期的な鍵の更新が可能になり、過去の鍵漏洩の影響をさらに減らすことができます。

• 通信セッション中に、新しい公開鍵ペアを交換
• 新しい公開鍵に基づいて、双方で新しいセッション鍵を生成

公開鍵（DH）ラチェットは、ルートKDF チェーンを2 回更新し、KDF出力キーを新しい受信および送信チェーンキーとして使用することから構成されます。

「ダブルラチェット」プロトコルは、前方秘匿性と将来秘匿性（post-compromise security）の両方を保証するために設計されています。

前方秘匿性: 新しいメッセージごとに異なる鍵が使われるため、過去の鍵が漏れても新しいメッセージは保護されます。

将来秘匿性: 公開鍵ラチェットによって、もしセッション中に秘密鍵が漏洩した場合でも、将来のメッセージは安全に保護され続けます。

Aliceのラチェットフロー

AliceとBobのラチェットフローイメージ

---

• 送受信ラチェットA1は以前に生成されたもの。
• AliceはラチェットA1で生成したメッセージ送信鍵でメッセージを暗号化して送信
• それを受信したBobは、ラチェットA1で生成したメッセージ受信鍵でメッセージを復号

---

• Bobは新たなセッションでメッセージを送受信するため、ラチェットDH1を実行し公開鍵をAliceに送信
• AliceはBobの新たな公開鍵と自身の新旧の秘密鍵からラチェットDH1を実行し、メッセージ送受信鍵の生成に必要なチェーン鍵（送受信の2種類）を生成
• ラチェットDH1により、メッセージ送受信鍵を生成するための送受信ラチェットA2,A3,A4,B1,B2を実行

---

• BobがメッセージA4を受信後、再びラチェットDH2を実行し公開鍵をAliceに送信
• AliceはBobの新たな公開鍵と自身の新旧の秘密鍵からラチェットDH2を実行し、メッセージ送受信鍵の生成に必要なチェーン鍵（送受信の2種類）を生成
• ラチェットDH2により、メッセージ送受信鍵を生成するための送受信ラチェットA5,B3,B4を実行

---

HKDF (HMAC-based Key Derivation Function)

HKDFは、HMAC（Hash-based Message Authentication Code） をベースにした鍵導出関数で、既存の秘密情報（例：共有鍵や乱数）から、暗号化や認証などに使用する鍵を生成します。

HKDFは以下の2つの主要なステップから成り立っています。

抽出フェーズ（Extract）:

入力となる秘密情報（乱数や共有鍵など）から、一貫した長さの「擬似乱数（PRK: Pseudo-Random Key）」を生成します。このプロセスには、HMACが使われ、入力データがHMACのハッシュ関数で「圧縮」されます。

拡張フェーズ（Expand）:

抽出フェーズで得られたPRKを基に、必要な長さの鍵素材を生成します。この拡張プロセスでもHMACを使います。

LinphoneのLIMEのHKDFでは、ルートキーとチェインキーを生成するHMACハッシュ関数（HKDF_RK, HKDF_CK）としてSHA512が導入されていています。

HKDF_RK

function KDF_RK(RK<32bytes>, DH_out<32, 56bytes>)
	info ← "DR Root Chain Key Derivation"
	RK<32bytes> || CK<32bytes> ← HKDFSha512(RK, DH_out, info)
	return RK<32bytes>, CK<32bytes>
end function

salt : RK(Root Key)
ikm : the output of ECDH(DH_out)
info : “DR Root Chain Key Derivation”
CK : Chain Key
Note) DH_out : X25519 >>> 32 bytes output, X448 >>> 56 bytes output, || means concatenation

function HKDFSha512(salt, ikm, info)
	return okm
end function

salt : optionnal
ikm : input key material
info : string
okm : output key material

HKDF_CK

function KDF_CK(CK<32bytes>)
	MK || IV ← HmacSha512(ChainKey, 0x01)
	CK ← HmacSha512(ChainKey, 0x02)
	return CK<32bytes>, MK<32bytes>, IV<16bytes>
end function

MK : Message Key
IV : Initialisation Vector
Note) || means concatenation

---

メッセージの暗号化と復号

ダブルラチェットプロトコルでは、各メッセージが新しい対称鍵で暗号化されます。
メッセージそのものを暗号化するためにAES-256-GCMが使用されます。

暗号化 : 送信者は、生成された対称鍵を使って、AES-256-GCMでメッセージを暗号化します。この際、GCMモードにより認証タグが生成されます。暗号化の際には、ノンス（nonce）または初期化ベクタ（IV: Initialization Vector） というランダムな値が必要です。

復号化 : 受信者は、受信したメッセージに対応する対称鍵をラチェットプロセスで生成し、AES-256-GCMを使ってメッセージを復号し、認証タグを確認することで改ざんされていないかチェックします。

メッセージの認証

AES-256-GCMは、単なる暗号化に加えて、メッセージの改ざんを防ぐための認証機能も備えています。GCM（Galois/Counter Mode） は、暗号化したデータの整合性を確認するために認証タグを生成します。

改ざん検知 : 受信者がメッセージを復号化するとき、暗号文に付随している認証タグを検証することで、メッセージが改ざんされていないことを確認できます。もし認証に失敗すれば、メッセージは破棄され、正しいデータを受け取ったかどうかが保証されます。

[tk-fuse]

EdDSAで署名されたSigned Pre Keyの生成・検証テスト

Pythonの仮想環境で実行

$ pyhon3 -m venv test
$ source test/bin/activate
(test) $ pip install --upgrade pip setuptools wheel
(test) $ pip install pynacl

eddsa.py

import nacl.signing
import nacl.encoding

# 1. 長期Identity Keyペアの生成
signing_key = nacl.signing.SigningKey.generate()  # 秘密鍵
verifying_key = signing_key.verify_key  # 公開鍵

# 2. PreKey（署名付き一時鍵）の生成
prekey_signing_key = nacl.signing.SigningKey.generate()  # 一時秘密鍵
prekey_verifying_key = prekey_signing_key.verify_key  # 一時公開鍵

# 3. PreKeyに対する署名（EdDSAで署名）
signed_prekey = signing_key.sign(prekey_verifying_key.encode())

# 4. 公開鍵の表示
print("Identity Public Key:", verifying_key.encode(encoder=nacl.encoding.HexEncoder).decode())
print("PreKey Public Key:", prekey_verifying_key.encode(encoder=nacl.encoding.HexEncoder).decode())

# 5. 署名の表示
print("Signed PreKey:", signed_prekey.signature.hex())

# 6. 署名の検証
try:
    verifying_key.verify(signed_prekey)
    print("署名の検証に成功しました。Signed PreKeyは正当です。")
except nacl.exceptions.BadSignatureError:
    print("署名の検証に失敗しました。")

(test) $ python3 eddsa.py
Identity Public Key: fa5988a3c7c02a8b9ab32e9f0bb39c01abbc7463302f5b2cb1704baac223b6b5
PreKey Public Key: 93a7c760addb474a7c957e01a2d07a89042ad349041be89919df671161e458c3
Signed PreKey: 6b5fdfb9621be3f470f309925d36658d0bd796e3def357da3c0f7b7c2586f9023d5dc3d9f43576e1df7527aac298a6584a23b21f001030b053d5600862b7fb06
署名の検証に成功しました。Signed PreKeyは正当です。

GitHub - pyca/pynacl: Python binding to the Networking and Cryptography...

Introduction | libsodium

---

https://asecuritysite.com/eddsa/eddsa2

メッセージmをPreKeyの公開鍵に置き換えて署名

Key generation

Alice generates a random 32-byte secret key (sksk) and then creates a public key of:

pk=sk⋅Gpk=sk⋅G

and where GG is the base point of the curve.

Signing

Alice creates a SHA-512 hash of her private key:

h=HASH(sk)h=HASH(sk)

Create rr from the upper 32 bytes of hash and the message:

r=HASH(h[32:]||m))r=HASH(h[32:]||m))

And where “||” represents a concatenation of the byte array values. Next she matches rr onto curve with:

R=r⋅GR=r⋅G

Next Alice computes ss with:

s=r+(HASH(R||pk||m))⋅sks=r+(HASH(R||pk||m))⋅sk

The signature is (R,sR,s). The values of RR and ss are 32 bytes long, and thus the signature is 64 bytes long.

Verifying

Bob creates SS using RR, pkpk and mm:

S=HASH(R||pk||m)S=HASH(R||pk||m)

And next creates two verification values:

v1=s⋅Gv1=s⋅G
v2=R+pk⋅Sv2=R+pk⋅S

If v1==v2v1==v2 the signature checks. This is because:

v1=sB=(r+(HASH(R||pk||m))⋅sk)⋅G=rG+sk⋅B⋅(HASH(R||pk||m))=R+pk⋅S=v2(mod q)